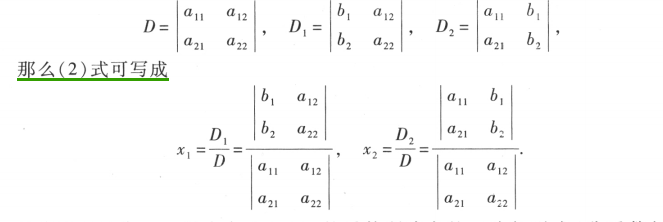第一章 行列式
二阶与三阶行列式
行列式的性质
*性质 1 行列式与它的转置行列式相等. *
*性质 2 对换行列式的两行(列) , 行列式变号 *
推论 如果行列式两行(列)完全相同,则此行列式为0
性质3 行列式的某一行(列)中所有的元素都乘以同一数k,等于k乘以这个行列式
推论 行列式中某一行(列)的所有元素的公因子可以提到行列式记号的外面
性质4 行列式中如果有两行(列) 元素成比例, 则此行列式等于零
性质5 若行列式的某一行(列) 的元素都是两数之和, 例如第 i 行的元素都是两数之和
性质 6 把行列式的某一行(列) 的各元素乘同一数然后加到另一行(列) 对
应的元素上去, 行列式不变
逆序数
对于 n 个不同的元素, 先规定各元素之间有一个标准次序(例如 n 个不同的
自然数, 可规定由小到大为标准次序), 于是在这 n 个元素的任一排列中, 当某一
对元素的先后次序与标准次序不同时, 就说它构成 1 个逆序.一个排列中所有逆
序的总数叫做这个排列的逆序数
上三角法求矩阵
等于主对角线的乘积
行列式按行(列)展开
行列式等于它的任一行(列)的各元素与其对应的代数余子式乘积之和
行列式某一行(列) 的元素与另一行(列) 的对应元素的代数余子式
乘积之和等于零
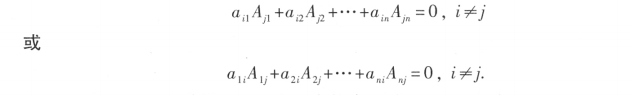
矩阵
当常数项 b1, b2, …, bm 不全为零时, 线性方程组(1) 叫做n元非齐次线性方程组.
n 元齐次线性方程组
n 元齐次线性方程组一定有零解,可能有非零解
元素是实数的矩阵称为实矩阵, 元素是复数的矩阵称为复矩阵
只有一行的矩阵A =(a1,a2… an)称为行矩阵, 又称行向量.
只有一列的矩阵称为列矩阵, 又称列向量*.
A 称为系数矩阵, x 称为未知数矩阵, b 称为常数项矩阵, B 称为增广矩阵
对角矩阵, 简称对角阵.对角阵也记作:
$$
A = diag(λ1, λ2, …, λn)
$$
位矩阵, 简称单位阵
矩阵运算
矩阵加法
(i) A +B = B +A;
(ii) (A +B) + C = A +(B +C)
数与矩阵相乘
(i) (λμ)A =λ(μA) ;
(ii) (λ +μ) A =λA +μA;
(iii) λ(A +B) =λA +λ B.
矩阵乘矩阵
定义4 设A=(ai)j 是一个m×s矩阵, B=(bi)j 是一个s×n矩阵, 那么规定矩
阵 A 与矩阵 B 的乘积是一个 m×n 矩阵 C =(cij)
必须注意: 只有当第一个矩阵(左矩阵) 的列数等于第二个矩阵(右矩阵) 的
行数时, 两个矩阵才能相乘
*总之, 矩阵的乘法不满足交换律, 即在一般情形下, A B≠ BA *
$$
(i) (A B) C = A(B C) ;
$$
$$
(ii) λ(A B) =(λA) B = A(λB) (其中λ 为数) ;
$$
$$
(iii) A(B + C) = A B +A C, (B + C) A = BA + CA.
$$
$$
对于单位矩阵 E, 容易验证E m A m × n = A m × n, A m × n E n = A m × n,或简写成E A = A E = A .
$$
矩阵的幂
$$
A kA l = A k+l, (A k) l = A kl
$$
$$
又因矩阵乘法一般不满足交换律, 所以对于两个 n 阶矩阵 A与 B, 一般说来(A B) k≠ A k B k, 只有当 A 与 B 可交换时, 才有(A B) k = A k B k
$$
例如(A +B) 2 = A 2 +2A B + B 2、 (A - B) (A + B) = A 2 - B 2 等公式, 也只有当 A与 B 可交换时才成立