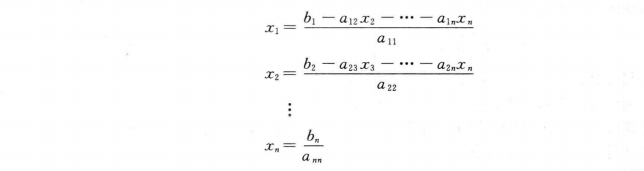
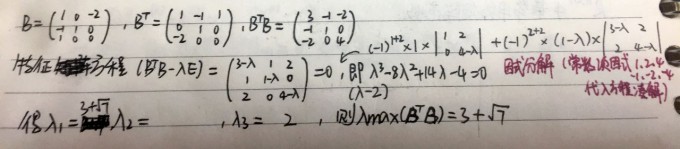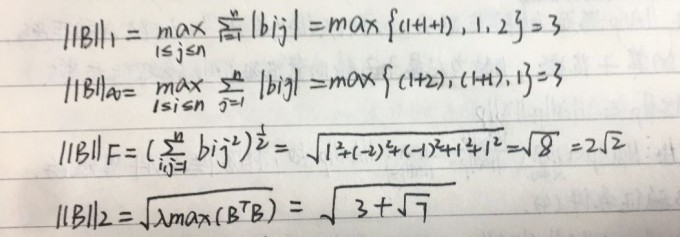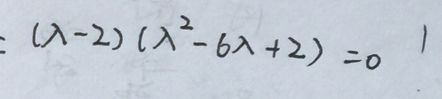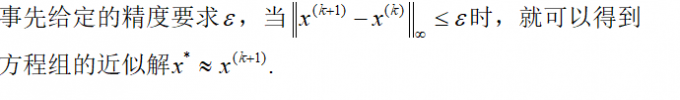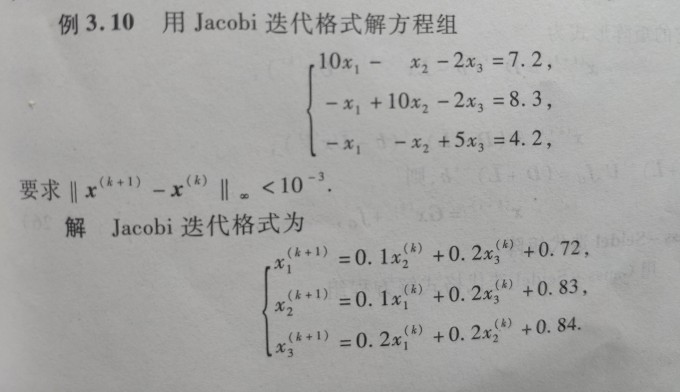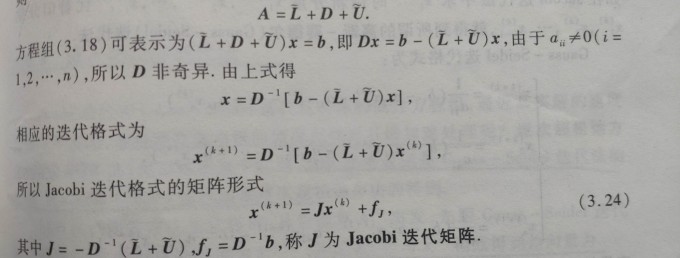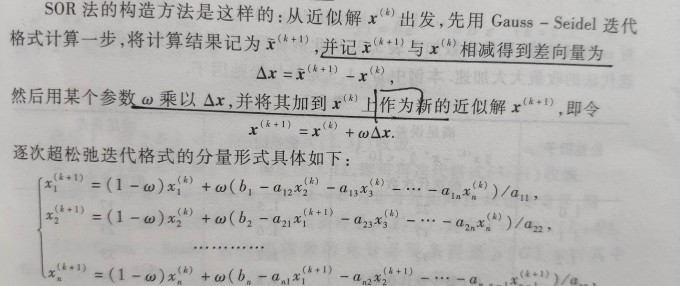方程组
高斯消去法
难于求解或求高精度的解
朴素的高斯消去法
主元:主对角线上的元素
步骤
消去步骤
代码

没有在aij的位置放零是因为后续不会用到该值,提高效率
当遇到主元为零是程序会终止
回代或向后求解
代码
操作次数
对消去步骤和回代步骤的计算次数进行统计
高斯消去法中消去步骤的操作次数
把第一列转化为0,需要(2n+1)(n-1)次计算:
(1+n+n)(n-1)

n个方程n个未知数的消去计算,可以在2/3n^3+1/2n^2-7/6n次操作后完成
复杂度
O(n^3)
高斯消去法中回代步骤的操作次数
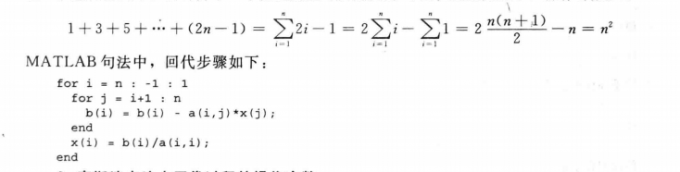
n个 方 程 n个 未 知 数 的 三 角 形 系 统 的 回 代 过 程 可 以 使 用 n^2次操作完成
*当n很大时,消去步骤的低阶可以省略; 换 句 话 说 , 对 于 “,在 复 杂 度 计 算 中 的 低 阶 项 对 于 算 法 运 行 时 间 的 估 计 没 有 大的 影 响 ,并可以忽略. *
例题
高斯主元素消去法
由高斯消去法知道在消元过程中可能出现的情况主元素为0,这时消去法将无法进行;即使主元素但很小时,用其作除数,会导致其他元素数量级的严重增长和舍入误差的扩散,最后也使得计算解不可靠
LU分解
LU分解过程
法一
在高斯消去法的基础上把0的位置写上倍数
法二
Amn = Lm1U1n + Lm2U2n + ...+ Umn
使用LU分解回代
1 | Ax = b |
复杂度
追赶法
在一些实际问题中, 例如解常微分方程边值问题,热传导方程以及船体数学放样中建立三次样条函数等,都会要求解系数矩阵为对角占优的三对角线方程组.
公式

例题


向量与矩阵的范数
向量范数
矩阵范数
例题
条件数.
与矩阵的范数有关

线性方程组的迭代方法
雅可比迭代法(Jacobi)
1.将线性方程组的第i个方程中的第i个变量用其它n-1个变量表示出来,生成迭代方程组
2.取定初始向量,依次迭代
3.
例题
Jacobi迭代格式矩阵形式
高斯-赛德尔迭代法(Gauss-Seidel)
对雅克比迭代法的改进,用以求出的新值代替旧值
例题
逐次超松弛迭代法(SOR)
针对收敛速度慢的情况。逐次超松弛迭代法是高斯-赛德尔的特殊情况
迭代法的收敛性
定理3.11(迭代法的基本定理): 对任意初值x(0)均收敛的充分必要条件是p(B) < 1
推论 2:
Jacobi迭代法收敛的充分必要条件是:
Gauss-Seidel迭代法收敛的充分必要条件是:
SOR